 | |||
| |||
Назад | Оглавление | ВпередРазделы А и Б настоящей работы посвящены теории роста кристалла, а в разделах В и Г рассматривается (в атомных масштабах) равновесная структура поверхности кристалла, находящегося в равновесии с паром. В разделе А вычисляется скорость перемещения мономолекулярных ступеней (т.е. краев недоукомплектованных мономолекулярных слоев кристалла) как функция пересыщения пара и средней концентрации изломов на ступени. Показано, что в большинстве случаев роста из паров скорость перемещения ступеней не зависит от их кристаллографической ориентации, вследствие чего замкнутая ступень роста имеет форму окружности. Определена так же скорость перемещения ряда параллельных ступеней и зависимость скорости перемещения ступеней от их кривизны. В разделе Б найдена результирующая скорость роста и ступенчатая структура конусов (или пирамид) роста, имеющих дислакационное происхождение. Рассмотрены случаи присутствия нескольких дислокаций; показано, что обычно они слабо отличаются от случая единичной дислокации. Установлено, что при малых пересыщениях скорость роста поверхности, содержащей дислокации, пропорциональна квадрату пересыщения, тогда как при больших значениях пересыщения эта зависимость становиться линейной. На основании этих выводов можно объяснить результаты измерений скоростей роста кристаллов йода из паров (Фольмер и Шульце [1]). Кратко обсуждается применение аналогичных методов к росту кристаллов из раствора. Раздел В настоящей работы посвящен исследованию равновесной структуры ступеней, в особенности статистике изломов на ступенях в зависимости от температуры, энергии связи и кристаллографической ориентации. Вычислена форма и величина двумерного зародыша (т.е. «острова» нового мономолекулярного слоя на кристаллической поверхности), находящегося в неустойчивом равновесии с паром при данных пересыщениях и температуре, и, следовательно, уточненное значение энергии активации для образования двумерных зародышей. При не слишком малых пересыщениях эта энергия так вклика, что совершенный кристалл не обладает заметной скоростью роста. Если на кристаллической поверхности имеется два выхода винтовых дислокаций противоположного знака, соединенных ступенью, то энергия активации весьма велика в том случае, когда расстояние между выходами меньше радиуса сответствующего критического зародыша, и равна нулю для несколько больших расстояний. В разделе Г рассматривается температурная зависимость структуры поверхности совершенного кристалла при учете явлений коллективного взаимодействия. Показано, что поверхность остается практически плоской (если не принимать во внимание одиночные адсорбированные молекулы и вакантные места на поверхности) до тех пор, пока не будет достигнута температура перехода, при которой шероховатость поверхности очень быстро возрастает («поверхностное плавление»). Если предположить, что все молекулы на поверхности могут находиться на одном из двух уровней, то оказывается возможным с небольшими изменениями использовать результаты Онзагера [2] для двумерных ферромагнетиков. Для граней со взаимодействием между ближайшими соседями в обоих направлениях [т.е. (100) для кубической решетки или (100) и (111) для гранецентрированной кубической решетки] температура перехода по порядку величины сравнима с температурой пловления кристалла. Если имеет место взаимодействие между вторыми ближайшими соседями, в одном из направлений [например, грань (110) простой кубической или гранецентрированной кубической решетки кристалла], то температура перехода будет ниже температуры плавления и будет соответствовать поверхностному плавлению связей между вторыми ближайшими соседями. Ошибка, связанная с предположением о существовании двух возможных уровней, исследована путем применения метода Бете [3], обобщенного на случай большего числа уровней. Для задачи с двумя уровнями упомянутый метод дает нормальный результат. Если учесть возможность существования трех уровней, то вычисленная температура перехода заметно уменьшается, однако при дальнейшем увеличении числа уровней она остается практически неизменной. Хотя между авторами настоящей работы имел место постоянный обмен идеями, однако наибольший вклад в раздел Б внес Франк, в то время как раздел Г, а так же все вычисления в разделах Б и В принадлежат исключительно Бартону и Кабрере. § 1. Движение ступеней на кристаллической поверхности. В течение последних 30 лет шло интенсивное развитие теории роста совершенного кристалла. Важные результаты в этой области получили Фольмер [4], Странский [5,6] Беккер и Деринг [7]. Еще раньше ряд существенных идей был высказан Гиббсом [8]. Согласно упомянутой теории, после исчезновения всех поверхностей высоких индексов кристалл продолжает расти благодаря возникновению на поверхности низких индексов двумерных зародышей новых молекулярных слоев. Как и во всех процессах, связанных с образованием зародышей, вероятность образования упомянутых двумерных зародышей сильно зависит от величины пересыщения. При пересыщениях меньших некоторого критического значения, эта вероятность пренебрежимо мала. Если же пересыщение больше коитического, то она очень быстро возрастает. Предположив разумное значение энергии боковой поверхности двумерного зародыша, можно показать, что ктитическое пересыщение составляет ~ 50%. При пересыщениях, достаточных для роста реальных кристаллов (1% и ниже), вероятность образования рассматриваемых зародышей должна быть, согласно этой теории, исчезающе малой (Бартон, Кабрера и Франк [9], Бартон, Кабрера [10], см. также раздел В настоящей статьи).
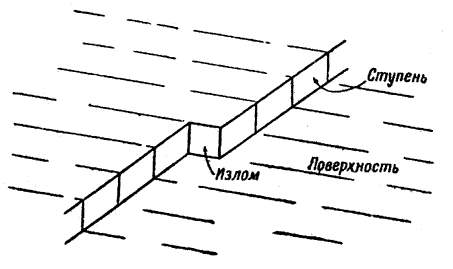
Рис. 1. Схематическое изображение ступени на поверхности и излома на ступени. Френкель [11] отметил, что поверхность реального кристалла при температуре выше абсолютного нуля должна иметь некоторую шероховатость, вызванную тепловыми флуктуациями. Рассматривая структуру мономолекулярной ступени, он пришел к выводу, что ступень имеет значительное количество изломов (рис. 1), понятие о которых было введено Косселем [12] и Странским [5,6]. Бартон и Кабрера [10] (см. также раздел В) установили, что концентрация изломов превышает значение, найденное Френкелем; этот результат весьма существенен для рассмотрения задачи о скорости перемещения ступеней (см. ниже). Френкель использовал идею тепловых флуктуаций и при рассмотрении структуры поверхности совершенного кристалла. Однако Бартон и Кабрера [10] (см. также раздел Г) показали, что ступени на гранях с низкими кристаллографическими индексами не могут быть вызваны термодинамическими флуктуациями. Такой процесс может происходить лишь вблизи точки плавления. Поэтому ступени, существование которых обязательно для продолжения роста, могут возникать на поверхности совершенного кристалла только в условиях высокого пересыщения. По нашему мнению, для объяснения роста кристаллов при низких пересыщениях необходимо предположить, что кристалл не является совершенным и что дефекты строения (в частности дислокации, имеющие в точке выхода на поверхность винтовую компоненту) приводят к образованию ступеней, благодаря чему отпадает необходимость возникновения двумерных зародышей. Эта идея, предложенная Франком (Бартон и др. [9], Франк [13]), развита в настоящей работе; мы покажем, что она объясняет многие особенности роста кристаллов при малых пересыщениях. Предлагаемая теория роста реального кристалла предполагает наличие в кристалле дислокаций, причем концентрация последних не существенна. Дальнейшее изучение роста кристаллов позволит, по-видимому, объяснить образование дислокаций, которые как и ступени на кристаллической поверхности, не могут возникать благодаря термодинамическим флуктуациям1). Хотя некоторые соображения относительно механизма образования дислокаций во время роста были высказаны Франком [13], однако подробной теории этих явлений еще не существует.