§ 4. Скорость перемещения ступени.
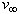 равна j/n0,
где 1/n0 — площадь, занимаемая одной молекулой. Поэтому
равна j/n0,
где 1/n0 — площадь, занимаемая одной молекулой. Поэтому
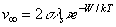 | ,(16) |
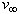 велико по сравнению с
характеристическим расстоянием lS; из (3), (5) и (16) имеем
велико по сравнению с
характеристическим расстоянием lS; из (3), (5) и (16) имеем
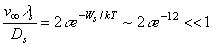 |
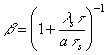 | ,(17) |
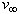 не будет зависеть от ориентации ступени. С другой стороны, если неравенство
lS>>x0 не выполняется, то
пересыщение около ступени не постоянно и будет функцией x0.
не будет зависеть от ориентации ступени. С другой стороны, если неравенство
lS>>x0 не выполняется, то
пересыщение около ступени не постоянно и будет функцией x0.
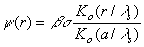 |
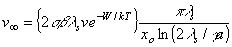 |
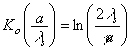 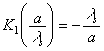 |
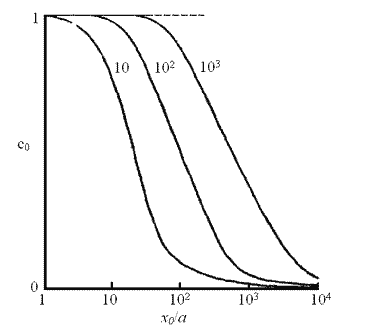
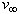 x0/a.
Используя (3) и (5), имеем
x0/a.
Используя (3) и (5), имеем
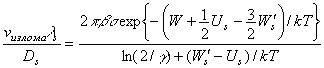 |
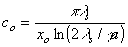 | ,(18) |
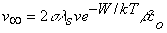 | ,(19) |
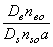 |
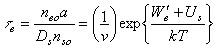 |
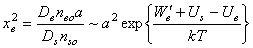 | ,(20) |
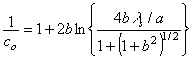 | , | 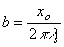 | ,(21) |
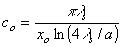 |
 | |||
| |||