Задача 1

В модели Лоренца найти действительную и мнимую части диэлектрической проницаемости сплошной среды, состоящей из осцилляторов с резонансной частотой w0. Учесть затухание. Построить графики зависимостей показателя преломления n(w) и показателя поглощения k(w) в окрестности резонанса. Возможна ли ситуация, когда n<1?

> restart;

На связанный электрон с зарядом q и массой m падает электомагнитная волна E(t) с поляризацией вдоль оси X, направленной вдоль оси осциллятора.

> E:=(t)->exp(I*w*t);

С учётом затухания (коэффициент b) получим уравнение колебаний осциллятора

> diff_eq:=Diff(x(t),t,t)+b*diff(x(t),t)+w0^2*x(t)=q*E(t)/m;

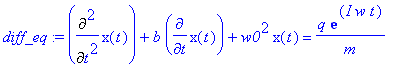
Незатухающее решение ищем в виде x(t)=A*exp(iwt)

> x(t):=A*exp(I*w*t);

> eq:=diff(diff(x(t),t),t)+b*diff(x(t),t)+w0^2*x(t)=q*E(t)/m;

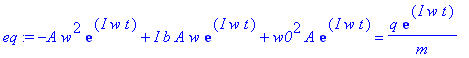
> A:=solve(eq,A);

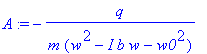
Поляризация единицы объёма вещества p=N*q*x(t), где N-концентрация осцилляторов

> p:=(t)->N*q*x(t);

Из уравнения D = E +4*Pi* P получим

> eq1:=p(t)=(epsilon-1)*E(t)/(4*Pi);

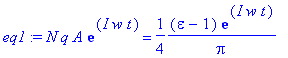
> epsilon:=solve(eq1,epsilon);

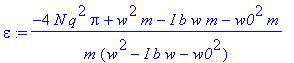
> equa:=convert(epsilon,parfrac,w);

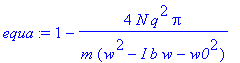
> epsilon1(w):=evalc(Re(equa));

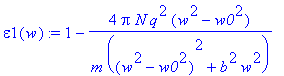
> epsilon2(w):=evalc(Im(equa));

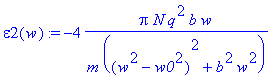
Запишем уравнения для коэффициента преломления n и коэффициента поглощения k

> eq3:=n^2-k^2=epsilon1;

> eq4:=2*n*k=epsilon2;

> k(w):=solve(eq4,k);

> eq5:=subs(k=k(w),eq3);

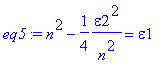
> solve(n^2*eq5,n);

Выберем корень, который не отрицателен и не может становится мнимым. Этот корень

> nroot(w):=sqrt(2*epsilon1+2*sqrt(epsilon1^2+epsilon2^2))/2;

> nroot(w):=subs(epsilon1=epsilon1(w),epsilon2=epsilon2(w),nroot(w));

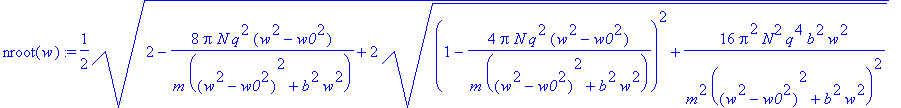
> nrootn(w):=subs({N=1,q=1,m=1,w0=1,b=1},nroot(w));

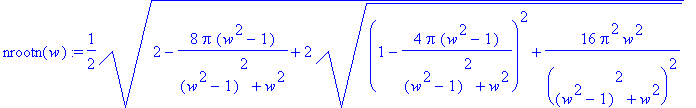
> plot(nrootn(w),w=0..10);

> kroot(w):=subs({n=nroot(w),epsilon2=epsilon2(w)},k(w));

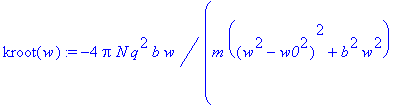
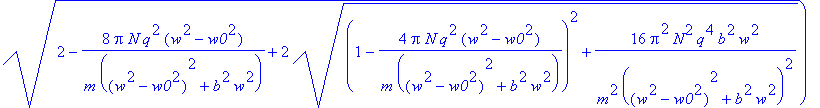
> krootn(w):=subs({N=1,q=1,m=1,w0=1,b=1},kroot(w));

>

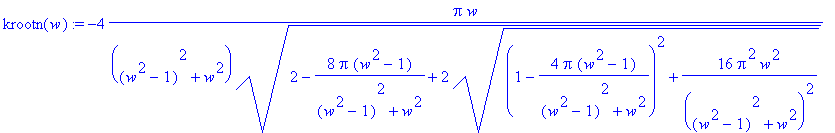
> plot(krootn(w),w=0..10);

>