МИНИСТЕРСТВО ОБЩЕГО И ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

РОССИЙСКОЙ ФЕДЕРАЦИИ

НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

Физический факультет

Кафедра общей физики

Емельянов Денис Юрьевич

ОТЧЕТ

о курсовой работе

“Рентгенографическое исследование летучего соединения АТ8, калибровка дифрактометра и измерение постоянной Авогадро”

Молекулярный практикум, 1 курс, группа 0372

Аннотация. Представлены теоретические основы метода рентгеновской дифрактометрии для исследования поликристаллов. Рассмотрен принцип работы дифрактометра типа ДРОН-RM4 (ИНХ СО РАН), на котором производились измерения. Проведена калибровка дифрактометра, измерены межплоскостные расстояния в образце АТ8, полученном осаждением летучего координационного соединения. Во второй части работы измерена постоянная Авогадро. Получено значение N_A=(6,021± 0,002)· 10²³ моль^-1, совпадающее в пределах погрешности с табличным значением. Работа относится к физике твердого тела.

1. Введение.

Цель работы—описание строения кристаллической решетки неизвестного образца, калибровка дифрактометра и измерение постоянной Авогадро. Калибровка дифрактометра необходима для повышения точности измерений межплоскостных расстояний. По известным межплоскостным расстояниям можно описать кристаллическую решетку вещества, из которого изготовлен образец. Знание кристаллической структуры вещества позволяет его идентифицировать.

2. Теоретическая часть.
1. Получение рентгеновских лучей.

Источником рентгеновского излучения является рентгеновская трубка. Пучок электронов с катода разгоняется высоким напряжением и ударяется в анод. При этом большая часть энергии пучка расходуется на нагрев анода (который охлаждается проточной водой) и лишь 2% преобразуется в рентгеновское излучение, состоящее из непрерывного и линейчатого спектров. Линейчатый спектр определяется материалом анода, поэтому он получил название характеристического.

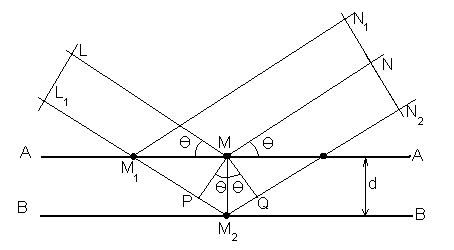
В зависимости от переданной атому энергии электрон переходит на более высокий уровень. Затем атом возвращается в прежнее состояние, при этом излучая квант определенной частоты. В зависимости от уровня возбуждения излучение разделяется на серии: K, L, M и т.д. Внутри каждой серии отдельные линии обозначаются греческими буквами. В рентгеновском дифракционном анализе используются линии Кa , Кb .

2. Формула Вульфа-Брэггов.

Рассмотрим две параллельные атомные плоскости АА и ВВ и падающий под углом q пучок рентгеновских лучей (см рис. 1). При этом атомы М, М₁, М₂ становятся источниками вторичного излучения. Вообще, рассеяние рентгеновских лучей идет во все стороны, но волны, рассеянные атомами М и М₁ усиливают друг друга в направлении, образующем с направлении, образующем с атомной плоскостью угол q . То же происходит с волнами, рассеянными любыми атомами плоскости АА, т.е. эту плоскость можно рассматривать как плоское зеркало.

Волна, рассеянная атомом М₂ будет усиливаться только в том случае, если длина ломаной PM₂Q, равная разности хода лучей LMN и L₁M₂N₂ , будет равна целому числу волн. Из геометрии, очевидно, что PM₂=M₂Q=d sinq . Отсюда можно получить условие для отражения волн от атомных плоскостей:

nl =2d sinq (1),

где n-целое неотрицательное число, l -длина волны рентгеновского излучения, d-межплоскостное расстояние.



Рис. 1. К выводу закона Вульфа-Брэггов.

3. Схема дифрактометра.

Расходящийся пучок рентгеновского излучения исходит из фокуса рентгеновской трубки F (см. рис. 2), затем проходит через щели Соллера S1, ограничивающие вертикальную расходимость и через систему щелей S2, S3. После отражения от образца пучок проходит через щели Соллера S4, щель S5 и попадает в приемную (аналитическую) щель S6, а затем через антирассеивающую щель S7 попадает на счетчик. Для сохранения фокусировки фокус рентгеновской трубки, ось образца и приемная щель должны в процессе съемки находиться на одной окружности переменного радиуса r =R/2sinq , где R—радиус гониометра.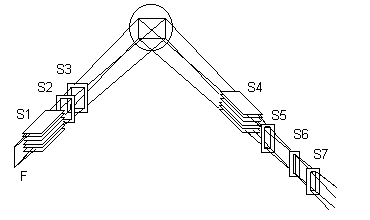



Рис. 2. Схема дифрактометра.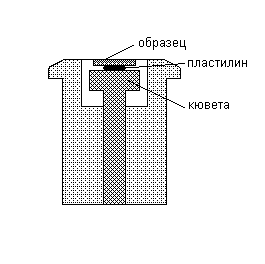

3. Рентгенографическое исследование.
1. Получение образца.

Образец АТ8, полученный осаждением летучего координационного соединения, представлял собой тонкий ровный слой на кремниевой подложке размером ~1´ 1 см. Эту подложку крепили при помощи пластилина на специальной кювете (см. рис. 3). Плоскость пластинки и верхней поверхности указанной кюветы совмещали с помощью стеклянной пластинки.

 

2. Предварительные эксперименты.
1. Измерение межплоскостных расстояний.

Эксперимент проводили на дифрактометре ДРОН-3М с фокусировкой по Брэггу-Брентано, радиус гониометра R=192 мм. Расходимость щелей Соллера—2,5 мм, ширина приемной щели—0,25 мм, фильтр—Ni, напряжение и ток на рентгеновской трубке—40 кВ и 22 мА, время интегрирования—0,5 с. Измерения угла 2q проводили в интервале от 5° до 30° со скоростью 2° /мин.

В эксперименте, помимо фона, связанного с кремниевой подложкой, наблюдались 4 дифракционных пика. Результаты эксперимента представлены в таблице 1.

Таблица 1.

Результаты измерений образца АТ8 на приборе ДРОН-3М.

2q , град.	q , град.	d*, Å.	hkl	c, Å.	d d, Å.
6,65	3,32	13,31	001	13,31	0,10
13,4	6,7	6,607	002	13,21	0,03
20,2	10,1	4,396	003	13,19	0,02

*- использована длина волны a _ср l =1,54178 Å.

2. Наблюдение b -составляющей в рентгеновском излучении.

Эксперимент проводился в аналогичных условиях. Единственное отличие состояло в отсутствии Ni-фильтра, благодаря чему были получены пики не только от Кa , но и от Кb линии.

Таблица 2.

Результаты измерений отражения (100).

	2q , град.	q , град.	d, Å.	d d, Å.
a	6,65	3,32	13,31*	0,10
b	6,00	3,00	13,30**	0,11

*- использована длина волны a _ср l a =1,54178 Å.

**- использована длина волны b l b =1,39217 Å.

3. Погрешности измерений.

Абсолютная погрешность измерения d определяется по формуле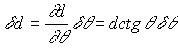

(2)

где d q - абсолютная погрешность измерения угла q , выраженная в радианах. При записи дифракционной картины на самописец (как это было в данном эксперименте) она определяется точностью измерений положения максимумов с помощью линейки - d q =0,025° =0,000436 рад. Из формулы (2) видно, что погрешность измерения d уменьшается с ростом угла q , поэтому для достижения максимальной точности следует использовать отражения в области больших углов.

3. Калибровка дифрактометра.

Дифрактометр ДРОН-RM4 (R=192 мм, CuKa -излучение, Ni-фильтр, детектор сцинтиляционный с амплитудной дискриминацией). В качестве внешнего эталона использован Si (a=5,4309 Å, l =1,540562 Å), приготовленный тонким (50-70 мм) слоем на полированной стороне стандартной кварцевой кюветы. Образец АТ8 представлял собой тонкий (1-2 мкм) слой вещества, полученный осаждением в вакууме на полированную пластинку Si. Пластинка крепилась в углублении стандартной кварцевой кюветы с помощью пластилина (см. рис. 4).



1. Съемка кремниевого эталона.

Съемка кремниевого эталона проведена в пошаговом режиме с временем накопления импульсов, достаточном для получения удовлетворительной статистики. Для пика (111) оно составляло 2 с, для (220) –10 с. Теоретические положения указанных отражений были соответственно 28,442 и 47,302. При определении положения максимума экспериментальных отражений использовали программу Origin. Пик сглаживали и обрабатывали с помощью дифференцирования полученной функции.

Калибровочный график для исследуемого интервала показан на рис. 5.



2. Рентгенографическое описание образца АТ8, как вторичного эталона.

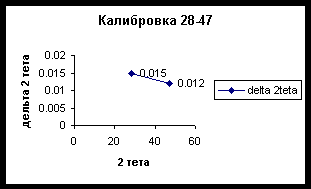
Съемка образца проведена в аналогичном режиме. Для пика (400), вошедшего в откалиброванный интервал была рассчитана величина 2q =2q _эксп+D 2q . Исходя из полученного значения, был рассчитан параметр а образца АТ8. Результаты измерений представлены в таблице 3. Теперь можно использовать этот образец в качестве вторичного эталона. Это представляет интерес, так как у него имеется ряд отражений в области <28° 2q .

Таблица 3.

Определение параметра а элементарной ячейки АТ8.

hkl	2q эксп, град	2q теор, град	а*, Å	d а, Å
400	27,181	27,196	13,115	0,009

*- использована длина волны a _ср l =1,54178 Å.

3. Калибровка дифрактометра в области малых углов.

Используя полученное значение а, были вычислены теоретические положения отражений (100), (200) и (300) и соответствующие величины D 2q =2q _теор-2q _эксп. Результаты измерений представлены в таблице 4, а калибровочный график для интервала углов 6-47° 2q показан на рис. 6.

Таблица 4.

Сопоставление теоретических и экспериментальных углов отражений АТ8.

hkl	2q эксп, град	2q теор, град	D 2q , град
100	6,703	6,739	0,036
200	13,477	13,502	0,025
300	20,267	20,312	0,045
400	27,181	27,196	0,015

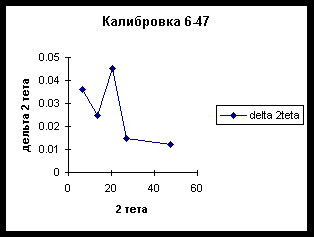Вид полученной калибровочной кривой говорит о том, что возможно не все экспериментальные факторы в нашем случае были идеальны. Это может относиться и к юстировке гониометра, и к приготовлению образца, и к методике проведения эксперимента.

4. Определение постоянной Авогадро рентгенографическим методом.
1. Методика измерения.

Плотность однородного вещества можно определить по формуле:

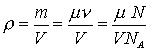(3),

где m -молярная масса, N –число молекул в объеме V, N_A- число Авогадро (число атомов в одном моле вещества).

Если в качестве V взять объем элементарной ячейки, то формула (3) преобразуется к виду: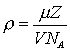

(4)

где Z - число атомов, приходящихся на одну элементарную ячейку.

Зная кристаллическую структуру вещества и определив параметры решетки, можно вычислить V и, затем, если известна плотность, рассчитать постоянную Авогадро.

В данной работе в качестве исследуемого вещества был использован кремний с кубической решеткой. Если обозначить параметр решетки через a, то число Авогадро вычисляется по формуле: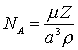

(5).

Рассмотрим кристаллическую решетку кремния (см. рис. 7). Каждый атом, находящийся в узле решетки принадлежит восьми элементарным ячейкам, атом, находящийся на грани куба—двум ячейкам и атом, находящийся внутри куба—одной ячейке. В элементарной ячейке первых атомов—8, вторых—6, третьих—4. Таким образом, на 1 ячейку приходится Z=8/8+6/3+4=8 атомов.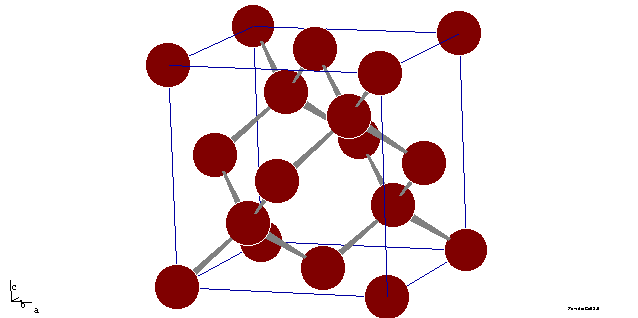



2. Описание эксперимента.

Измерение параметра элементарной ячейки кремния было проведено по положению дифракционного отражения (331). Для этого в пошаговом режиме был записан (дифрактометр ДРОН-RM4, R=192 мм, CuKa -излучение, детектор сцинтиляционный с амплитудной дискриминацией) интервал углов от 75 до 78° 2q с шагом 0,02° и временем накопления 30 с. На рис. 8 отчетливо видно разделение дублета линий a ₁ и a ₂, что позволяет использовать длину волны одной из них.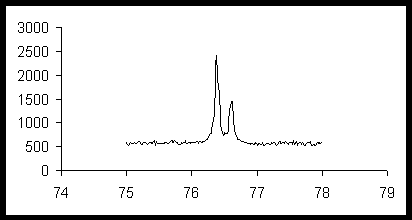



Рис. 8. Дифрактограмма кремния.

 

 

3. Результаты измерения.

Результаты измерений представлены в таблице 5

Таблица 5.

Результаты измерения постоянной Авогадро.

2q , град	q , град	d, A	hkl	a*, A	NA, моль-1
76,380	38,190	2,4917	331	5,4306	6,0210· 1023

*- использована длина волны a ₁ l =1,540562 Å.

Для расчета параметра решетки a была использована программа Excel. При расчете числа Авогадро по формуле (3) были использованы табличные значения плотности кремния r =2,33 г/см³ и молярной массы m =28,0855 г/моль.

4. Погрешности измерений.

Абсолютная погрешность измерения d вычисляется по формуле(2). Параметр решетки а прямо пропорционален d, поэтому формула для d a получается из формулы (2) заменой d на a:

d а=аctgq × d q (6)

При d q =0,01° погрешность составила d а=0,0018A . Погрешность определения числа Авогадро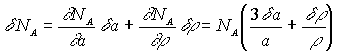

(7)

При d r =0,005 г/см³ значение d N_A=0,002× 10²³ моль^-1.

5. Результаты.

В результате работы получен калибровочный график для дифрактометра ДРОН-RM4 в интервале углов 6- 47° 2q , определен параметр элементарной ячейки летучего соединения АТ8- а=13,115± 0,009 Å, получено значение постоянной Авогадро N_A=(6,0210± 0,0022)× 10²³ моль^-1.

6. Выводы и заключение.

Проведенная калибровка позволяет проводить более точные измерения на данном дифрактометре, причем погрешность измерения падает с увеличением угла отражения. Полученное значение постоянной Авогадро совпадает в пределах погрешности со справочным значением 6,022045× 10²³ моль^-1[4].

1. Л.М.Ковба, Рентгенография в неорганической химии. М.: Изд-во МГУ, 1991. 256 с.
2. Ч. С.Баррет, Т.Б.Массальский, Структура металлов. М.: Металлургия, 1984. 686 с.
3. В.И Лисойван, С.А. Громилов, Аспекты точности в дифрактометрии поликристаллов. Новосибирск, Наука, 1989. 243 с.
4. Н.Л. Глинка. Общая химия. Ленинград: Химия, 1988. 702 с.